Das Signifikanzniveau ist eine wichtige Größe bei der Durchführung von statistischen Tests. Ein anderer gängiger Ausdruck ist Irrtumswahrscheinlichkeit. Hintergrund ist der Umstand, dass bei statistischen Tests Fehler nicht ausgeschlossen werden können, sondern Ergebnisse stets nur mit einer bestimmten Wahrscheinlichkeit korrekt sind. Das Festlegen eines Signifikanzniveaus bei einem statistischen Test ist gleichzusetzen mit dem Festlegen eines zu tolerierenden Fehlers.
Inhaltsverzeichnis
- 1 Signifikanzniveau „einfach erklärt“
- 2 Definition: Signifikanzniveau
- 3 Auswahl des Signifikanzniveaus
- 4 Der Hypothesentest des Signifikanzniveaus
- 5 Vergleich des Signifikanzniveaus und p-Werte
- 6 Die statistischen Ergebnisse des Signifikanzniveaus und p-Wertes
- 7 Die richtige Beurteilung der Signifikanz
- 8 Häufig gestellte Fragen
- 9 Quellen
Signifikanzniveau „einfach erklärt“
Wenn man eine statistische Analyse durchführt, vergleicht man die Daten mit der Nullhypothese, um zu entscheiden, ob man sie ablehnen oder nicht ablehnen kann. Das Signifikanzniveau gibt an, wie groß die Wahrscheinlichkeit sein muss, dass ein beobachteter Unterschied oder Effekt tatsächlich auf etwas anderes als Zufall zurückzuführen ist, damit man die Nullhypothese ablehnen kann.
Definition: Signifikanzniveau
Wenn Du einen statistischen Test durchführst – beispielsweise einen Chi Quadrat Test – dann definierst Du zunächst die Nullhypothese H0. Für die Auswertung des statistischen Tests ist das Signifikanzniveau relevant. Entsprechend den Regeln des gewählten statistischen Tests erfolgen die Ablehnung oder die Annahme der Nullhypothese. Das Ergebnis des statistischen Tests ist signifikant, wenn die Daten in einem hohen Maße auf ein Abweichen von der Nullhypothese hinweisen.
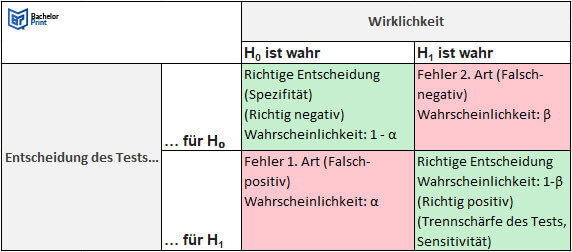
Das Signifikanzniveau beschreibt die Wahrscheinlichkeit, mit der eine zutreffende Hypothese irrtümlich verworfen werden könnte. Es handelt sich um den Fehler 1. Art. Es wird zwischen dem Fehler 1. Art und dem Fehler 2. Art unterschieden. Ein Fehler 1. Art liegt bei falsch positiven Ergebnissen vor. Wird die Alternativhypothese H1 irrtümlich zurückgewiesen, dann liegt ein Fehler 2. Art vor.
Das Signifikanzniveau beschreibt ausschließlich den gewählten zulässigen Fehler, nicht jedoch die Stärke der Effekte.
In der Praxis wird in diesem Kontext oftmals der p-Wert fehlinterpretiert. Der p-Wert induziert die statistische Signifikanz. Es handelt sich um den Signifikanzwert. Der p-Wert ist das kleinste Signifikanzniveau, bei dem die Nullhypothese abgelehnt werden kann. Als Wahrscheinlichkeit nimmt der p-Wert Werte zwischen 0 und 1 an. Da der falsche Umgang mit dem p-Wert dermaßen verbreitet war, veröffentlichte die American Statistical Association im Jahr 2016 eine Mitteilung, die sich der statistischen Signifikanz widmete.
Auswahl des Signifikanzniveaus
Für Hypothesentests wird üblicherweise ein Signifikanzniveau von 5 Prozent oder von 1 Prozent gewählt. Ein Signifikanzniveau von 1 Prozent impliziert eine größere Strenge, da die Toleranzgrenze für den Fehler 1. Art (= Alpha-Fehler) herabgesetzt ist. Für kleinere Studien und im studentischen Kontext ist ein Signifikanzniveau von 5 Prozent die häufigste Wahl. Lediglich bei großen Datenmengen solltest Du 1 Prozent als Signifikanzniveau wählen.
Alpha-Fehler entstehen, wenn die Datenauswertung auf das Ablehnen der Nullhypothese hinweist, die Nullhypothese aber eigentlich exakt zutrifft.
Ein Beispiel:
Die Nullhypothese lautet: „Der Patient leidet nicht an der Krankheit X.“
Ein Alpha-Fehler liegt vor, wenn irrtümlicherweise angenommen wird, der Patient leide an der Krankheit X. Die Nullhypothese wird irrtümlicherweise verworfen. Weist ein durchgeführter Test auf das Vorliegen der Krankheit X hin, dann besteht dennoch die Möglichkeit, dass der Patient gesund ist.
Der Hypothesentest des Signifikanzniveaus
Hypothesentests werden in der Praxis mittels Software-Unterstützung durchgeführt. Ein häufig verwendetes Programm ist SPSS. Das statistische Programm ermöglicht die Auswertung von Datensätzen, beispielsweise mittels t-Test, Chi Quadrat Test oder Regressionsanalyse. Basierend auf einem gewählten Signifikanzniveau werden Hypothesentests durchgeführt, wobei eine Nullhypothese und eine Alternativhypothese aufgestellt werden.1
Führst Du einen Chi Quadrat Test nach Pearson mittels SPSS durch, dann erhältst Du in der Tabelle folgende Angaben:
- Wert
- df
- Asymptotische Signifikanz (zweiseitig)
- Exakte Signifikanz (2-seitig)
- Exakte Signifikanz (1-seitig)
Für die Interpretation der Ergebnisse sind vor allem der Wert, der Freiheitsgrad (=df) und die Asymptotische Signifikanz (= p-Wert) relevant. Signifikanz wird im Allgemeinen angenommen, wenn der p-Wert unterhalb von 5 Prozent liegt – bei strengen Hypothesentests unterhalb von 1 Prozent.
Stichprobe & Grundgesamtheit
Die Grundgesamtheit umfasst alle Elemente beziehungsweise Individuen, für die Ergebnisse gelten. Da es nicht möglich ist, alle Elemente der Grundgesamtheit zu berücksichtigen, wird eine Stichprobe gewählt. Die Stichprobe repräsentiert die Grundgesamtheit, sie wird stellvertretend für die Grundgesamtheit betrachtet. Es ist wichtig, eine ausreichend große Stichprobe zu wählen und darauf zu achten, dass die Stichprobe tatsächlich für die Grundgesamtheit repräsentativ ist.
Ein Beispiel:
Im Rahmen eines statistischen Tests soll überprüft werden, ob ein Zusammenhang zwischen Rauchen und dem Auftreten der Krankheit X besteht. Die Grundgesamtheit umfasst alle Menschen, sowohl Raucher als auch Nicht-Raucher. Aus Kostengründen ist es nicht möglich, alle Menschen in der Studie zu berücksichtigen. Daher wird eine Stichprobe von beispielsweise 1.000 Menschen ausgewählt – sie bilden die Gruppe der Probanden für die Studie.
Wie formuliere ich die Hypothese?
Die Nullhypothese wird durch den statistischen Test überprüft. Ein Beispiel für eine Nullhypothese lautet:
- Nullhypothese: „Es besteht kein Zusammenhang zwischen der Körpergröße und dem Geschlecht.“
Die Alternativhypothese bildest Du ausgehend von der Nullhypothese:
- Alternativhypothese: „Es besteht ein Zusammenhang zwischen der Körpergröße und dem Geschlecht.“
Vergleich des Signifikanzniveaus und p-Werte
Das Signifikanzniveau legst Du vor der Durchführung des statistischen Tests fest. Du definierst dadurch die Strenge des Tests. Die p-Werte berechnen sich aus den vorliegenden Daten. Du findest den p-Wert in den von SPSS erstellten Tabellen, zumeist ausgewiesen als Signifikanz. Ob Du die Nullhypothese verwirfst oder annimmst, hängt von der Frage ab, ob das Ergebnis signifikant ist und ob der Wert die Nullhypothese bestätigt.
Ein Beispiel:
Du führst einen Chi Quadrat Test durch. In der Tabelle überprüfst Du, ob das Ergebnis signifikant ist. Außerdem vergleichst Du den berechneten Wert mit dem kritischen Wert der Chi Quadrat Tabelle. Du liest den kritischen Wert passend zum gewählten Signifikanzniveau und den vorhandenen Freiheitsgraden ab.
Die statistischen Ergebnisse des Signifikanzniveaus und p-Wertes
Das Ergebnis des Chi Quadrat Tests formulierst Du so:
„Ein Chi-Quadrat-Test wurde zwischen Geschlecht und Körpergröße durchgeführt. Es besteht ein statistisch signifikanten Zusammenhang zwischen Geschlecht und Körpergröße, X²(df) = Wert, p = …, Phi-Koeffizienten = ….
Die richtige Beurteilung der Signifikanz
Bei der Durchführung und der Interpretation statistischer Tests sind von besonderem Belang:
- Wahl eines günstigen Signifikanzniveau
- Zusammensetzung der Stichprobe
- Beurteilung des Werts des statistischen Tests
- Test bietet keine 100-prozentige Sicherheit sondern nur basierend auf dem Signifikanzniveau
- Datensatz vorher überprüfen
Häufig gestellte Fragen
Du wählst das Signifikanzniveau aus, meistens 1 Prozent oder 5 Prozent.
Das Signifikanzniveau ist der Fehler 1. Art beim statistischen Test. Es gibt an, mit welcher Wahrscheinlichkeit eine zutreffende Nullhypothese irrtümlicherweise abgelehnt wird.
Je größer Du das Signifikanzniveau wählst, denn weniger zuverlässiger sind die Ergebnisse.
Für die Bestimmung des kritischen Wertes berücksichtigst Du das Signifikanzniveau, Du liest den gesuchten Wert in der Tabelle bezogen auf das Signifikanzniveau und die Freiheitsgrade ab.
Das Signifikanzniveau hat direkte Auswirkungen auf die Stärke eines statistischen Tests. Wenn das Signifikanzniveau niedrig ist, ist die Wahrscheinlichkeit, dass die Nullhypothese fälschlicherweise abgelehnt wird, geringer. Dies bedeutet, dass der Test strenger ist und ein stärkerer Beweis für die Alternativhypothese erbracht werden muss.
Quellen
1IBM: Tests auf Unabhängigkeit (Chi-Quadrat), in: Ibm.com, 22.03.2021, [online] https://www.ibm.com/docs/de/spss-statistics/25.0.0?topic=SSLVMB_25.0.0/spss/tables/sig_tests_chisq_ex.html (abgerufen am 05.04.2023)
2Statista: Definition Grundgesamtheit, in: De.statista.com, o.D., [online] https://de.statista.com/statistik/lexikon/definition/60/grundgesamtheit/ (abgerufen am 05.04.2023)